Calculating Electronic Resonances with Complex-Valued EOM-CC Methods
-
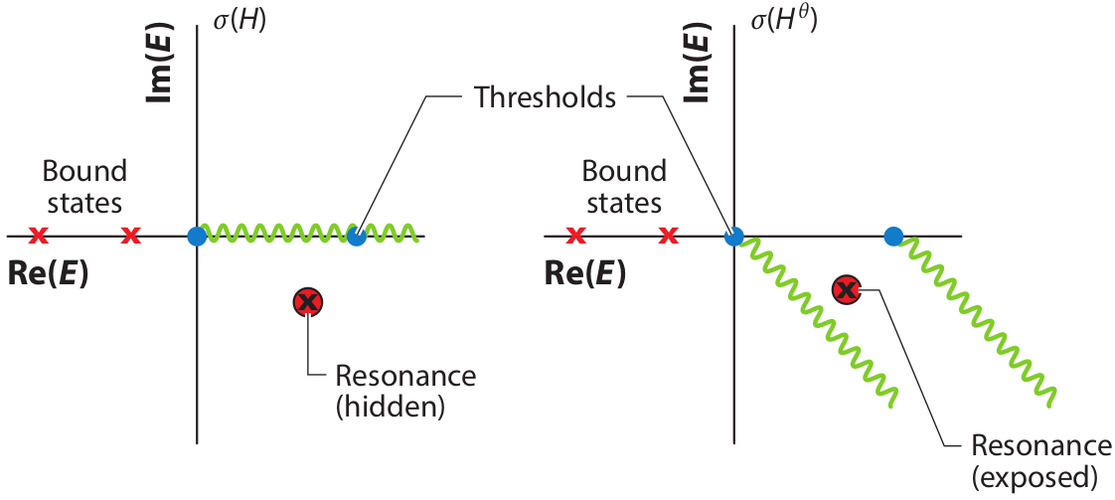
Resonances are electronically unbound states; they are metastable and decay by ejecting an electron.
-
Resonances are embedded in the continuum and are not accessible by standard quantum-chemistry methods.
-
Within non-Hermitian quantum mechanics, resonances become \(L^2\)-integrable, discrete states with complex energies (the real part describes resonance position and the imaginary part describes the resonance width); this enables calculation of resonances by standard quantum chemistry methods.
-
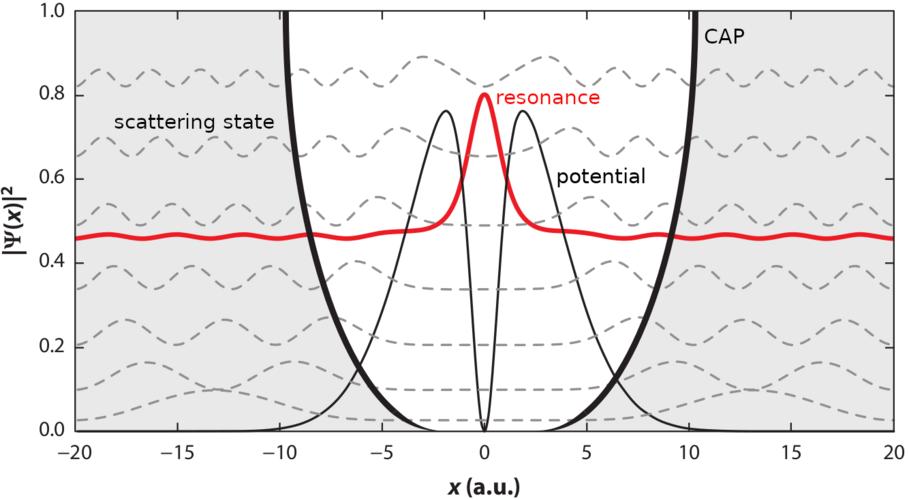
Non-Hermitian extensions of quantum chemistry include 1) scaling all coordinates of the Hamiltonian with a complex factor exp(i*\(\theta\)) (the complex-scaling method); 2) using complex basis functions; 3) augmenting the Hamiltonian by a local complex absorbing potential i*\(\eta\)*W(r).
-
EOM-CC methods provide an excellent platform for treating resonances because they efficiently include correlation and tackle multiple electronic states of different character in a balanced fashion.
-
Energies, properties, and nuclear gradients are available for several complex-valued EOM-CC methods.
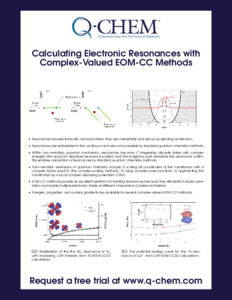
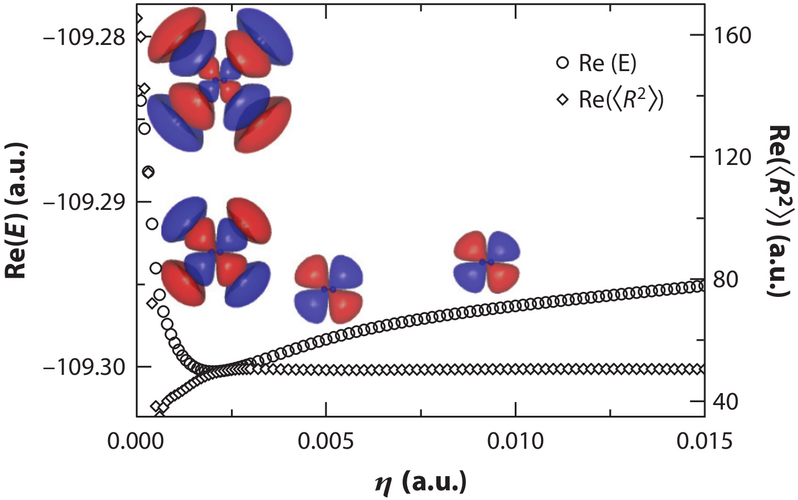 Stabilization of the the 2\(\Pi_g\) resonance of N\(_{2}^{-}\) with increasing CAP intensity from EOM-EA-CCSD calculations
Stabilization of the the 2\(\Pi_g\) resonance of N\(_{2}^{-}\) with increasing CAP intensity from EOM-EA-CCSD calculations
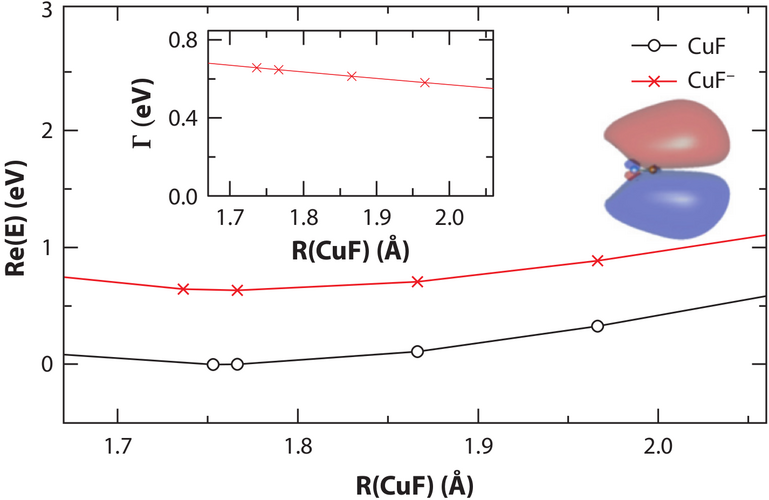 The potential energy curve for the \(^2\Pi\) resonance of CuF\(^{-}\) from CAP-EOM-CCSD calculations
The potential energy curve for the \(^2\Pi\) resonance of CuF\(^{-}\) from CAP-EOM-CCSD calculations
Want to try Q-Chem?